本文梳理了期权的核心基础、定价模型、风险度量工具(希腊字母)及实际交易应用。详解了Black-Scholes定价公式的原理与参数应用,深入剖析了Delta、Gamma、Vega、Theta、Rho五大希腊字母的定义、性质及交易指导意义,为期权交易的定价分析、风险监控与策略构建提供了理论基础。
期权的定义与类型
期权是持有人在特定时间(欧式:到期日;美式:到期日前任意时间)以固定价格买卖资产的权利。分为看涨期权(Call)与看跌期权(Put),具体差异如下表:
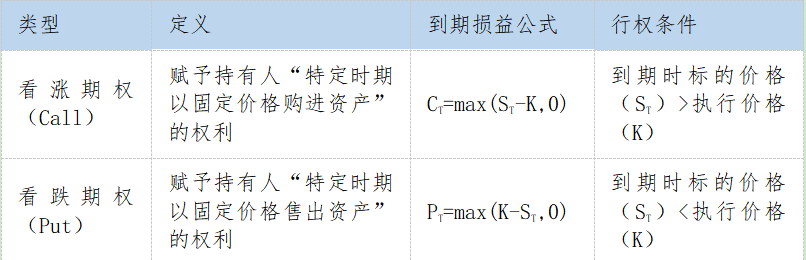
二、期权平价公式
对于同一标的、同一行权价K、同一到期日T的欧式期权(且标的资产在期权存续期内无股息支付),其认购期权(Call)价格c、认沽期权(Put)价格p、标的资产现价及行权价现值之间存在如下精确的无套利定价关系:c Ke-rT=p S
通过无套利定价和复制资产的方法推倒如下:
构建两个投资组合:
组合A:一份欧式认购期权加上在T时刻收益为K的零息债券
组合B:一份欧式认沽期权加上一单位标的资产S
认购期权、认沽期权的执行价格为K,期限为T。组合A当前的价值是欧式认购期权的价值c和零息债券的价值Ke-rT;组合B当前的价值是欧式认沽期权在当前的价值p和标的资产S。
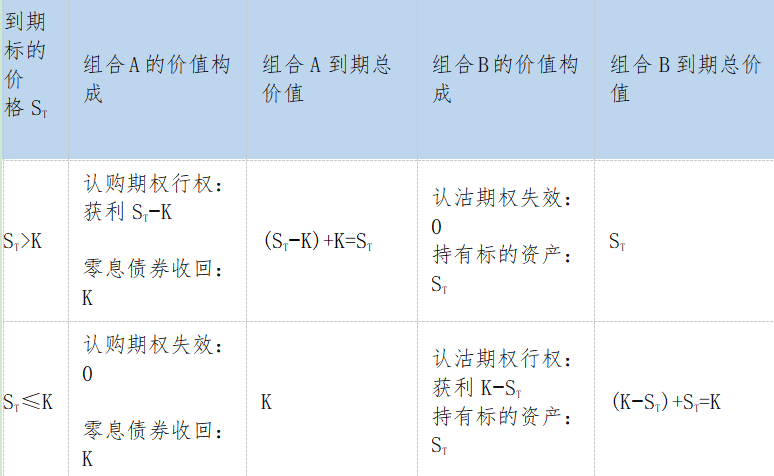
结论:无论在何种市场情形下,组合A与组合B在到期日T的价值均为 max(ST, K)。根据无套利原则,它们当前的构建成本(即现值)必须相等:c Ke-rT=p S
它表明欧式认购期权的价值可根据相同行权价格和到期日的欧式认沽期权的价值推导出来;反之,欧式认沽期权的价值也能通过相同行权价和到期日的欧式认购期权推导出来。
三、Black-Scholes定价公式
1、欧式看涨期权定价公式:
C=S0N(d1)−Ke-rTN(d2)
2、欧式看跌期权定价公式:
P=Ke-rTN(−d2)−S0N(−d1)
其中:N (・):标准正态累积分布函数;d1、d2为推导得出的中间变量,与 S、K、r、σ、T 相关
C,P:看涨、看跌期权理论价格
S0:标的资产当前价格
K:行权价
T:到期时间
r:无风险利率
σ:标的资产年化波动率
3、定价原理与价值构成
核心逻辑:Black-Scholes公式可以理解为期权到期损益在风险中性概率测度下的期望,即C=e-rTE[max(ST-K,0)],P=e-rTE[max(K-ST,0)]。
价值构成:
内在价值:立即行权的收益,看涨为max(S-K,0),看跌为max (K-S,0)。
时间价值:期权价格超出内在价值的部分,受波动率、到期时间影响,波动率越高、到期时间越长,时间价值越高。
四、希腊字母:期权风险的量化指标
希腊字母用于衡量 “标的价格、波动率、时间、利率” 等因素变动对期权价值的影响,核心指标如下表:

许妍(投资咨询证号:Z0020627) 作者单位:兴业期货
免责声明: 上述信息均来源于公开资料,我公司对这些信息的准确性和完整性不做任何保证,也不保证所包含的信息和建议不会发生任何变更,我们已力求报告内容的客观、公正,但文中的观点、结论和建议仅供参考,投资者据此做出的任何形式的任何投资决策与本公司和作者无关。 上述内容版权仅为我公司所有,未经书面授权,任何机构和个人不得以任何形式翻版、复制发布。如引用、刊发,须注明出处为兴业期货,且不得对本报告进行有悖原意的引用、删节和修改。











